Hash-Based Signatures: A Quantum-Resistant Future?

Beyond RSA & ECDSA: The Future of Digital Signatures in a Post-Quantum World

Introduction

In Cryptography, digital signatures are the means of verifying the authenticity of digital messages and documents, so what exactly are digital signatures? They function like handwritten signatures but offer much more security and can be easily verified and stored securely in cyberspace, reducing the risk of theft or loss. In this post, I’ll be explaining the different Hash-based signature schemes used in modern-world cryptography.

Background

Digital signatures serve as the foundation of public-key cryptography. A digital signature scheme is a type of public key cryptography where a user (i.e. the signer) creates a pair of keys (private and public key ). Creating a digital signature, σ involves the signer signing the message using his private key. the signer then appends the resulting signature σ to m and sends the pair (σ,m) to the verifier. The verifier can then verify the authenticity of the message with the help of public key.

Traditional digital signature schemes such as RSA (Rivest Shamir Adleman) and ECDSA (Elliptical Curve Digital Signature Algorithm ) are used in SSL/TSL to ensure secure data transmission. However, with the rise of quantum computing, these traditional signatures face significant threats, For instance, RSA relies on the assumption that factoring the product of two large prime numbers is computationally infeasible with classical computers. Similarly, ECDSA is based on the hardness of computing discrete logarithms. While these assumptions hold true for current systems, using Shor’s algorithm , quantum computers can efficiently solve these problems, posing a serious risk to existing cryptographic signature schemes.¹

Now that we understand the need for quantum-proof signatures, the next question is: How do we achieve this level of security? There are several candidates that can fulfil the requirements of post-quantum signatures; however, in this post, I’ll focus exclusively on Hash-Based Signatures, a type of digital signature scheme that uses hash functions as its central building block.

Why Hash Functions?

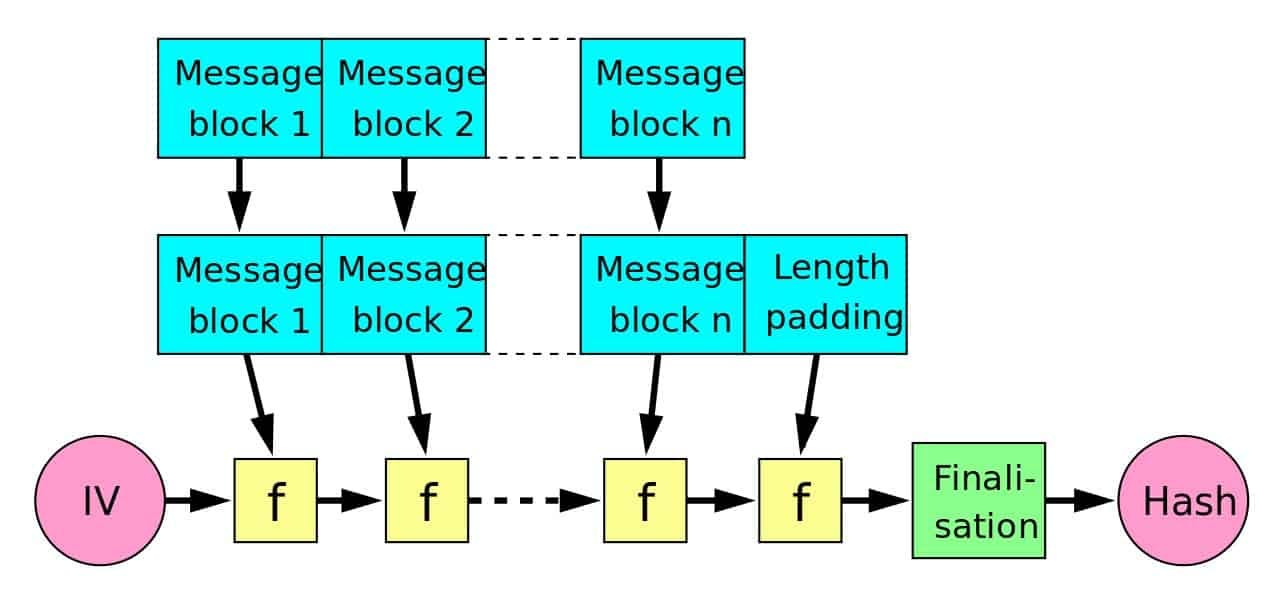
Hash functions are a one-way function that produces a constant size output given arbitrary-sized input. To understand how hash functions work and answer why they can be used in Post-quantum secure schemes, let’s look at SHA2, a family of hash functions.

The mechanism by which SHA-2 calculates the output is explained as follows. First, the input data are expanded into message blocks. Each message block is used to update the value of the internal state. With an initial value as the start point, the final output (hash value) is computed by repeatedly updating the internal state many times by using the message blocks. Since hash functions such as SHA-2 do not have a neat algebraic structure like that of prime factorization, it has been thought that they would not be immediately breakable even with the advent of quantum computers.

Source: https://www.comparitech.com/blog/information-security/what-is-sha-2-how-does-it-work/

Hash-Based Signature Schemes

Hash-based signature schemes can be majorly classified into two main types :

• OTS (One-time Signature): Can only be used once per key pair

• Few-time Signature: Can be used multiple times per key pair without compromising the security of the scheme

All the protocols consists of 3 algorithms (Kg,Sign,Ver)

i) Key Generation : (pk,sk) ←Kg(κ)

ii) Signature: σ←Sign (m,sk)

iii) Verification : 0/1 ←Ver(m,σ,pk)

Note: In the entire post, I’ll be using the following conventions →

\(pk: Public \ Key \quad sk: Private\ Key \quad m: Message \quad σ: Signature\)

Lamport OTS

This was the first hash-based signature scheme solely based on hash functions. Let's imagine that we possess a hash function H that can transform a 256-bit input into a 256-bit output.

\(H: \{0,1\}^{256} \rightarrow \{0,1\}^{256}\)

Say we aim to sign messages of length 256 bits (If less than that, the message can be padded to form 256 bits ), then our first step will be the Key Generation step.

LOTS.Kg

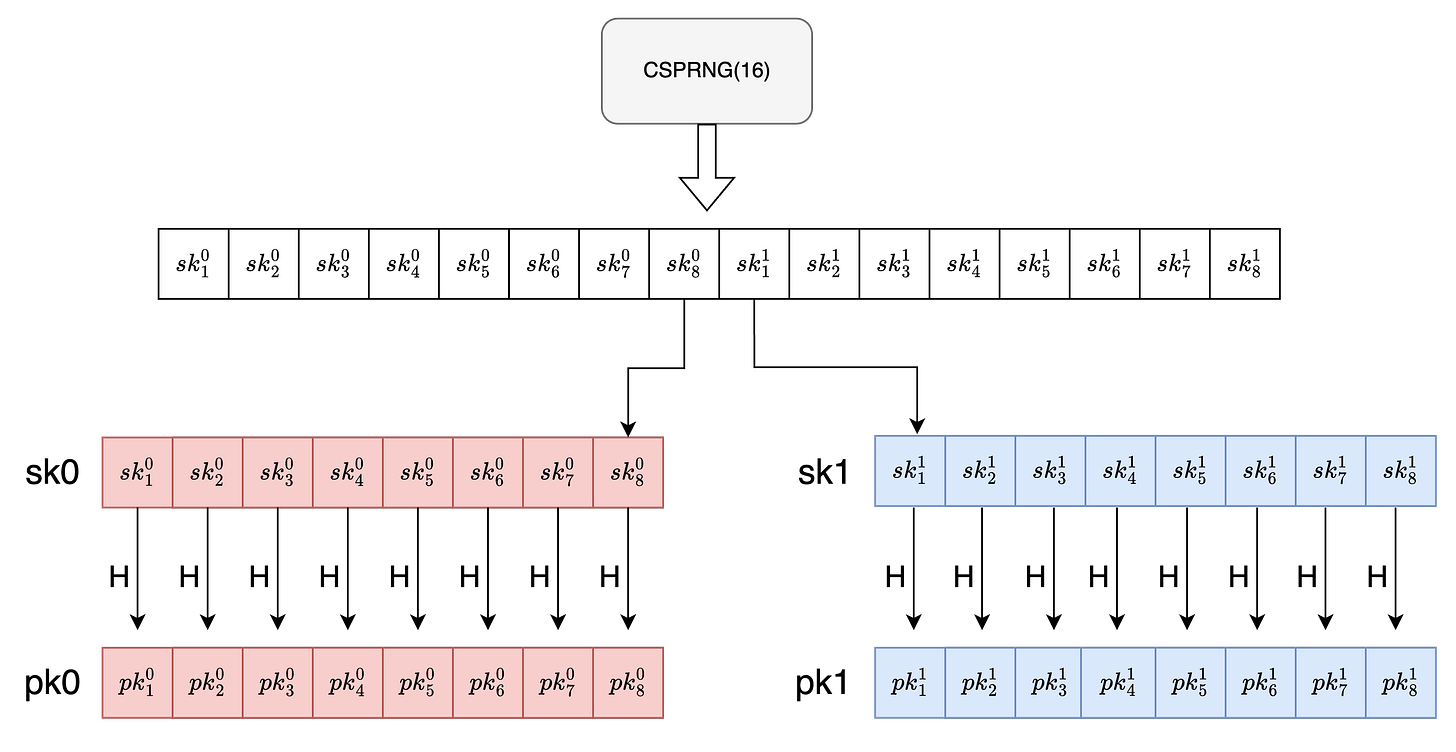
To generate our private key, we produce 512 randomised bit sequences , each being 256 bits in length, using a cryptographically secure pseudo-random number generator (CSPRNG), which is an algorithm that produces high entropy random numbers of the desired bits.

\(CSPRNG: {n} \rightarrow \{0,1\}^{n}\)

Out of these 512 sequences , the initial 256 are concatenated to form the first secret key, sk0 and the remaining 256 are used to form sk1. Therefore sk is represented as tuple (sk0,sk1) .

\(sk_0=sk_1^0 || sk_2^0 || sk_3^0 || ...... || sk_{255}^0 || sk_{256}^0 \)

\(sk_1=sk_1^1 || sk_2^1 || sk_3^1 || ...... || sk_{255}^1 || sk_{256}^1 \)

\(\text{Note that each } sk^j_i , \ i \in \{1,256\} ,j \in \{0,1\} \text{ is } 256 \text{ bits in length}\)

To compute the public keys we’ll be hashing all the above individual 512 sequences using the earlier introduced hash function H. Similar to sk0 and sk1 , the initial 256 of the hashed values are concatenated to form pk0 and the remaining 256 are used to form pk1.

\(pk_0=H(sk_1^0) || H(sk_2^0) || H(sk_3^0) || ...... || H(sk_{255}^0) || H(sk_{256}^0 ) \)

\(pk_1=H(sk_1^1) || H(sk_2^1) || H(sk_3^1) || ...... || H(sk_{255}^1) || H(sk_{256}^1 ) \)

Now that we (as a signer) have successfully generated key pairs , we can hand over our public key to the entire world (The verifier in our case ), however we must keep the private key a secret .

\(sk=(sk_0,sk_1) \quad pk=(pk_0,pk_1)\)

LOTS.Sig(m,sk)

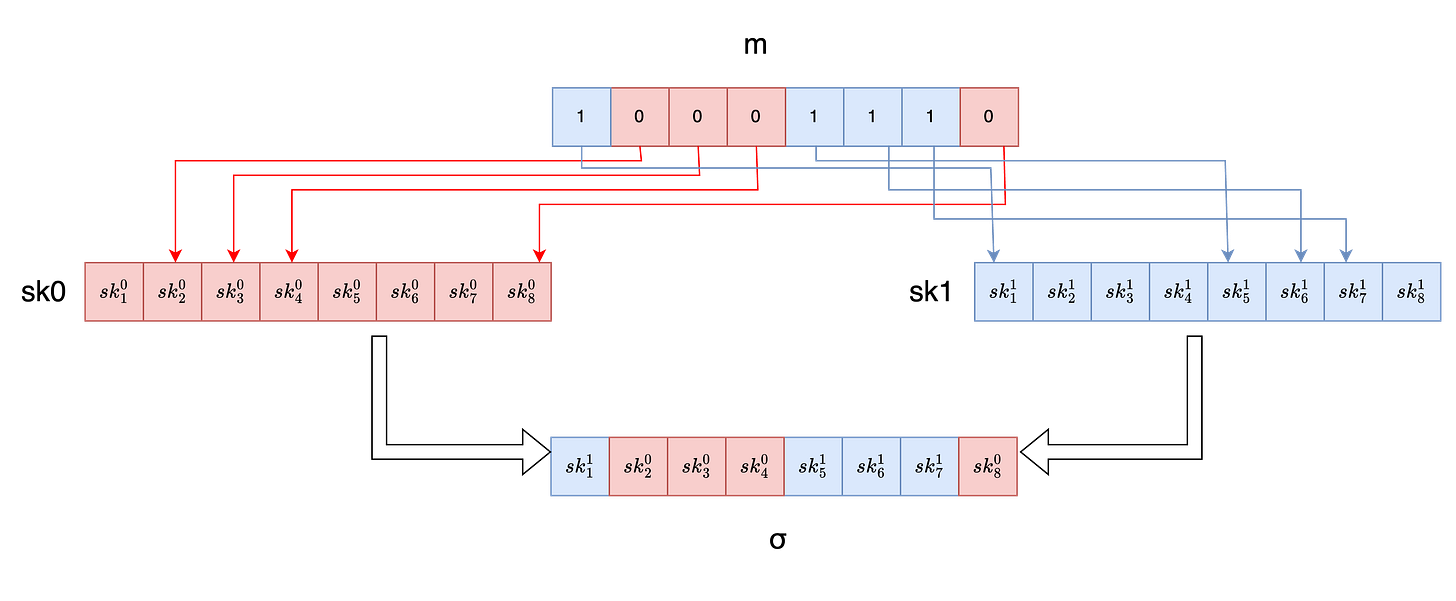
To sign our message and generate the corresponding signature we represent m as a sequence of 256 bits , then for each i ∈ {1,256}:

• If the ith message bit i.e mᵢ equals 0 then we grab the ith secret key string from sk0 list, and output that string as part of our signature

• If mᵢ equals 1 then we include the ith secret key from sk1 list as part of our signature

\(m=m_1||m_2||m_3||......||m_{255}||m_{256} \)

\(m_i \in \{0,1\} | 1 \leq i \leq 256\)

Concretely, for i=1 to 256:

\(\text{if } m_i == 0 \text{ then } σ_i=sk^0_{i} \quad \)

\(\text{else } σ_i=sk^1_{i} \quad \)

\(σ=σ_1||σ_2||σ_3||......||σ_{255}||σ_{256}\)

We concatenate all the output signature chunks to form the signature σ of our original message m.

LOTS.Ver(σ,m,pk)

After we generate the signature , we’ll send the signature and public key to the verifier (or receiver of the message ) along with the message itself , the verifier can then proceed to check the authenticity of the message that is to ensure the message was indeed signed by the sender and has not been tampered with.

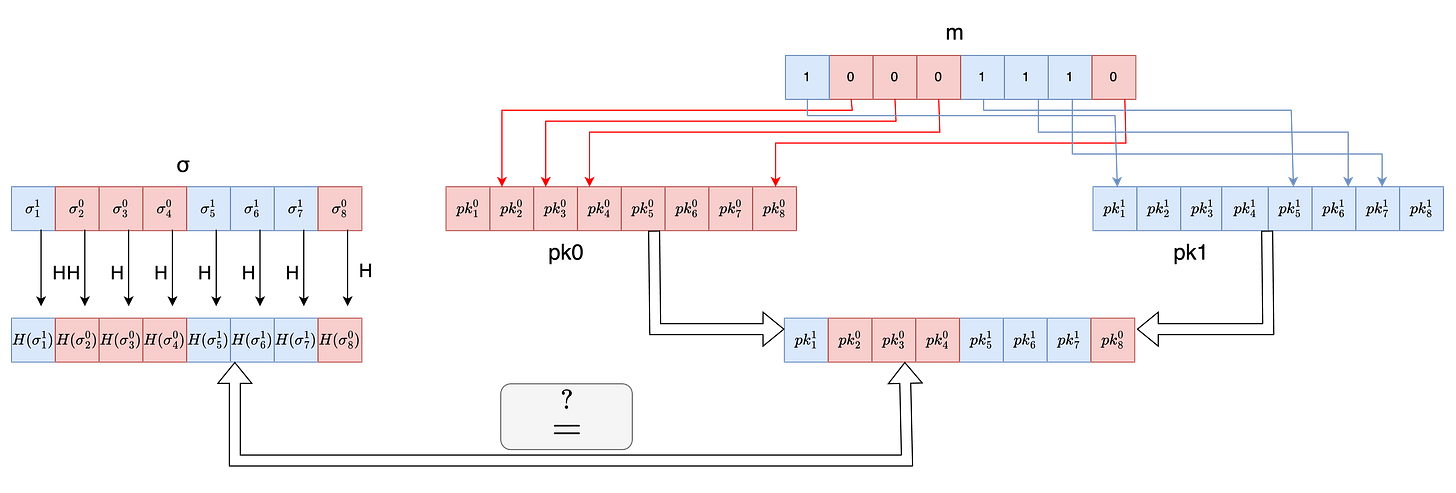
For each individual signature chunk σᵢ where i ∈ {1,256} ,the verifier computes the hash H(σᵢ)

• If mᵢ equals 0 verifier checks that the computed value H(σᵢ ) equals ith public key string from pk0 .

• If mᵢ equals 1 verifier checks if H(σᵢ ) equals ith public key string from pk1.

\(\text{if } m_i == 0 \text{ then } H(σ_i)\stackrel{?}{=}pk^0_{i} \)

\(\text{else } H(σ_i)\stackrel{?}{=}pk^1_{i} \)

Since the verifier proceeds iteratively so for any i if the verification fails , the verifier returns 0 , and if the verification passes for all i ∈ {1,256} the verifier returns 1 .

Note that during the signing process, the private key was used to generate the signature, while in the verification process, the public key was used to validate the signature. This highlights a fundamental aspect of digital signatures, explaining the literal definitions of public and private keys. The private key must always remain secret, ensuring that only the rightful owner can sign messages, while the public key is shared openly, allowing anyone to verify the authenticity and integrity of the signed message. This mechanism forms the foundation of secure communication, authentication, and non-repudiation in cryptographic systems.

Toy-Example

Below figure shows an illustration of how Lamport-OTS works , For simplification I have taken a 8-bit message instead of 256-bits , and secret key is formed by sixteen 256-bit integers as shown below . Secret key is then hashed to form public key . The secret key is then used to generate signature . The generated signature along with the message and public key is then sent to verifier , who then verifies the authenticity of the message . The signature is then shared with the verifier along with the message and public keys and the verifier can then proceed with the verification process .

• Kg

• Sig

• Ver

Winternitz OTS

A drawback of Lamport OTS is the huge size of signatures and key pairs , in Winternitz signature scheme we try to reduce these sizes at the cost of additional hash evaluations.

We’ll be using a chain function c to compute successive hash evaluations.

\(c^i(x,r)=F(c^{i-1}(x,r) \oplus r_i)\)

\(c^0(x,r)=x\)

Here F is a hash function similar to H in Lamport-OTS however instead of fixating on 256 bits it can take arbitrary n-bit input and generate n-bit output.

\(F: \{0,1\}^{n} \rightarrow \{0,1\}^{n}\)

x serves as input message whose successive hashes need to be calculated and r is the bitmask that adds security enhancement through randomisation.

\(x \in \{0,1\}^n \quad \quad r_i \in \{0,1\}^{n}\)

The XOR operation randomises the input to the hash function at each step that prevents an attacker from computing multiple chains simultaneously.

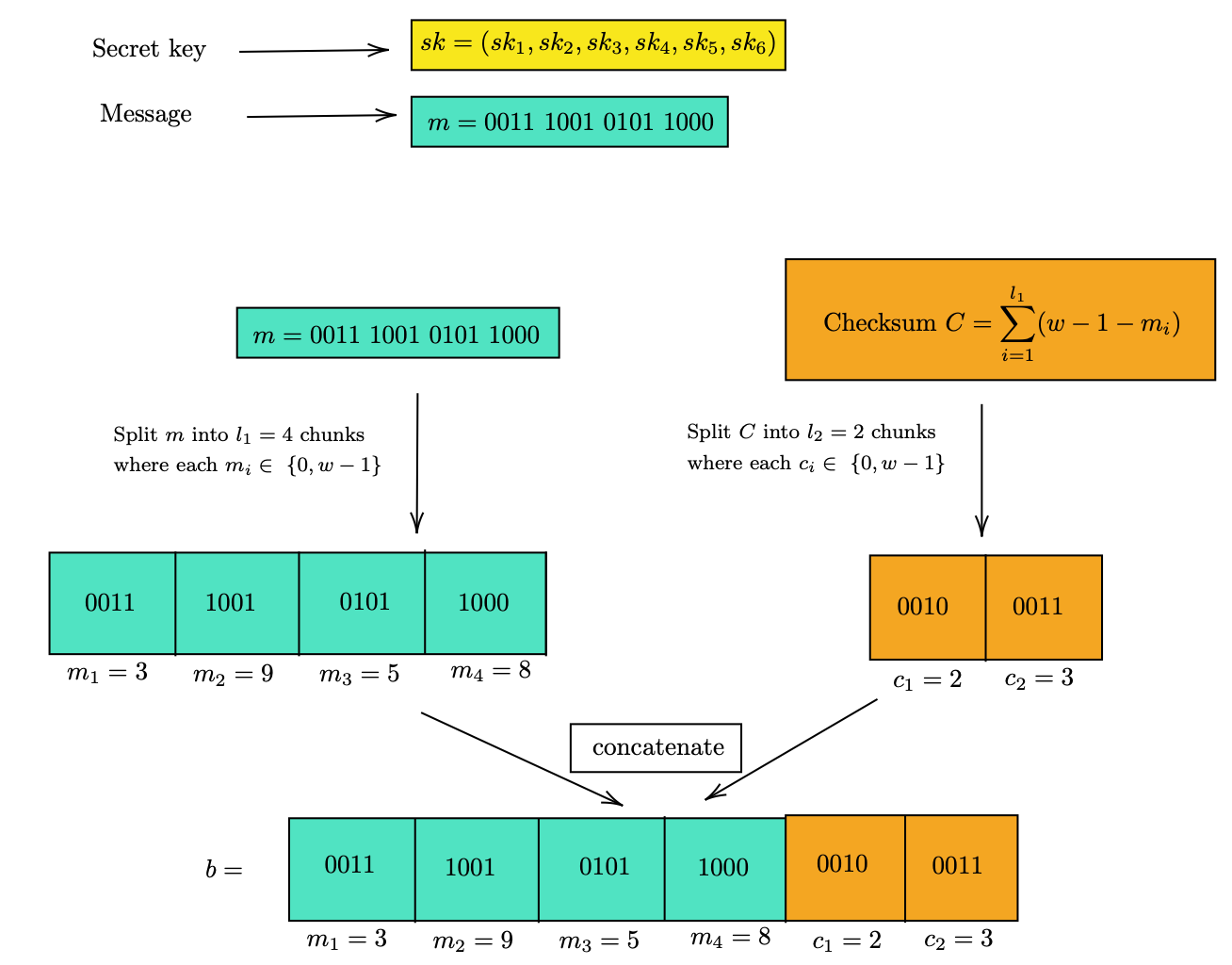
²W-OTS first converts the n-bit message into base w representation which provides us several chunks of message each of length log(w) bits. The number of these chunks equals n/log(w) . Here w is configurable and

• Larger w creates less amount of message chunks and thus shorter signatures but higher computation (we’ll soon see how )

• Smaller w creates more amount of message chunks and requires less computation( at the cost of larger space )

\(n-bit \ message\ m \ => m_1||m_2||m_3||......m_{{l_1}-1}||m_{l_1} \)

\(m_{i} \in \{0,w-1\}\ | \ 1 \leq i \leq l_1 \ | \quad l_1= {\lceil}\frac{n}{log_2(w)}{\rceil}\)

There also exists a checksum C which is essential to prevent signature forgery which will be explained later.

\(C=\Sigma^{l_1-1}_{i=1}(w-1-m_i) \)

The computed sum C is then represented as a list base w chunks.

\(C=C_1||C_2||C_3||......||C_{l_2-1}||C_{l_2}\)

\(C_{i} \in \{0,w-1\}\ | \ 1 \leq i \leq l_2 \ | \quad l_2=\lceil \frac{{\lfloor}log_2{(l_1(w-1))}{\rfloor}}{log_2(w)}+1 \rceil\)

The maximum value of the checksum C is when all message digits are 0

• In this case, each term (w-1-mᵢ) equals (w-1)

• There are l₁ such terms, so the maximum value is l₁(w-1)

• The number of bits needed to represent l₁(w-1) is ⌊log₂(l₁(w-1))⌋ + 1

  • The +1 ensures we have enough bits even when l₁(w-1) is a power of 2

• Converting from bits to base-w digits requires dividing by log₂(w) and rounding up

  • Thus, l₂ = ⌈(⌊log₂(l₁(w-1))⌋ + 1)/log₂(w)⌉

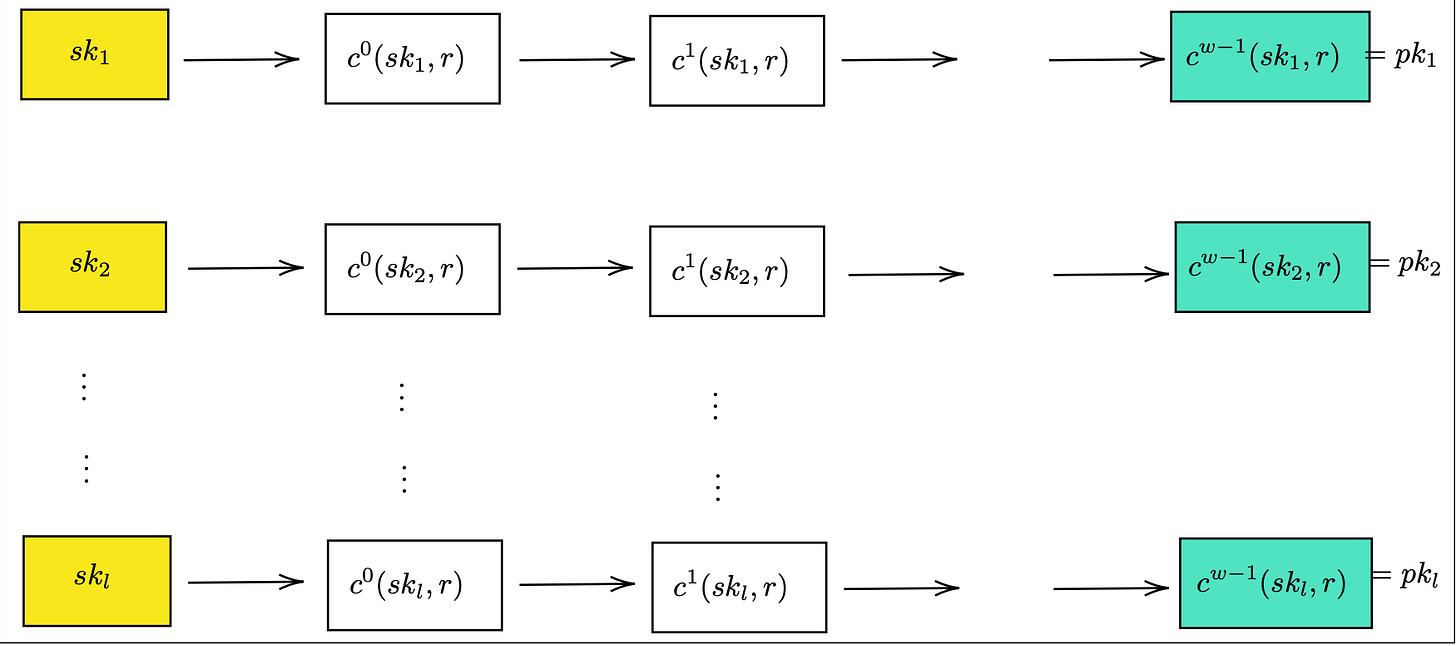
WOTS.Kg(S,r,l)

For secret key generation we use a pseudo random number generator G , which is different from the one used in L-OTS .Instead of generating pairs for each of the message bit (a total of 2n secret keys), it generates a single value per message segment. A message segment comprises of log(w) bits. Thus making it a much more efficient key generation process than the one in previous protocol.

The secret key sk is generated by applying G to the seed S (secret n-bit string) to produce l distinct n-bit strings.

\(G_l{(S)} = sk=sk_1||sk_2||sk_3||......||sk_{l-1}||sk_l\)

\(S \in \{0,1\}^n \quad sk_i \in \{0,1\}^n \)

G is typically implemented as any cryptographic hash function H applied to the seed concatenated with an index i.

\(sk_i=G(S,i)=H(S||i) \quad \quad 1 \leq i \leq l\)

\(l=l_1+l_2\)

Number of secret key components equals the sum of the total chunks in message m and checksum C.

The signer then derives the public keys by applying the chain function (w-1) times on the l secret keys generated.

\(pk=pk_1||pk_2||pk_3||......||pk_{l-1}||pk_l\)

\(pk_i=c^{w-1}(sk_i,r) \quad \quad 1\leq i\leq l\)

\(r=r_1||r_2||r_3||......||r_{w-2}||r_{w-1} \quad \quad r_i \in \{0,1\}^n \quad \quad 1\leq i \leq w-1\)

\(c^j(sk_i,r)=F(c^{j-1}(x,r) \oplus sk_i)\)

Here's what's happening:

\(\text{For all secret keys} \ sk_i \ 1\leq i \leq l \)

1. The previous chain value cj−1(skᵢ,r) is XORed (⊕) with the current bitmask value rᵢ

2. The result of this XOR operation is then fed into the hash function F

3. This produces the next value in the chain cj(skᵢ,r)

WOTS.Sign(m,sk)

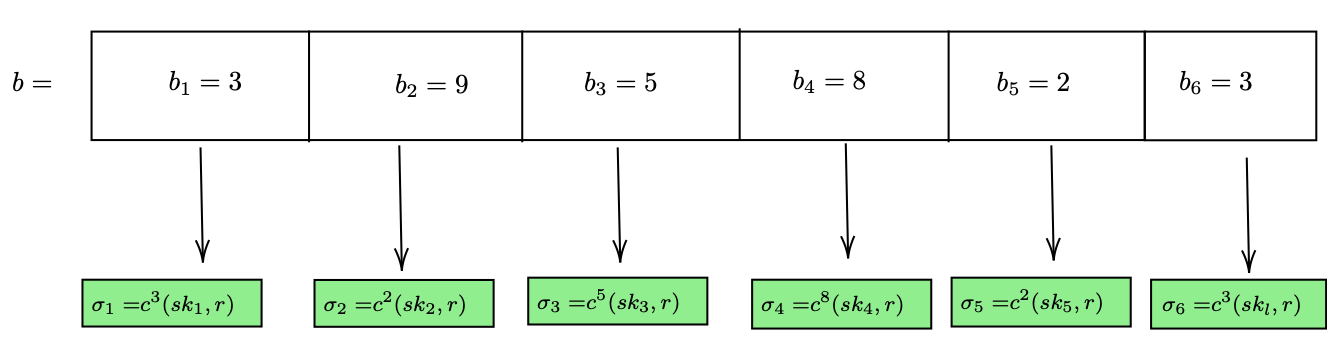
The l1 chunks of message and l2 chunks of checksum C are then concatenated to form string b of length l (= l1 + l2). Each of the individual chunks of b are represented as base-w.

\(b \ = \ ( b1||b2||b3||.......||b_{l-1}||b_l) \ = \ ( m1||m2||......||m_{l_1}||C_1||C_2||......||C_{l_2})\)

\(b_i \in \{0,w-1\} \quad 1\leq\ i \leq l\)

The signature of m can then be computed by successively hashing each secret key component as many times as the corresponding matching segment in the base-w representation of b using the chain function.

\(\sigma=c^{b_1}(sk_1,r)||c^{b_2}(sk_2,r)||c^{b_3}(sk_3,r)||......||c^{b_{l-1}}(sk_{l-1},r)||c^{b_l}(sk_l,r)\)

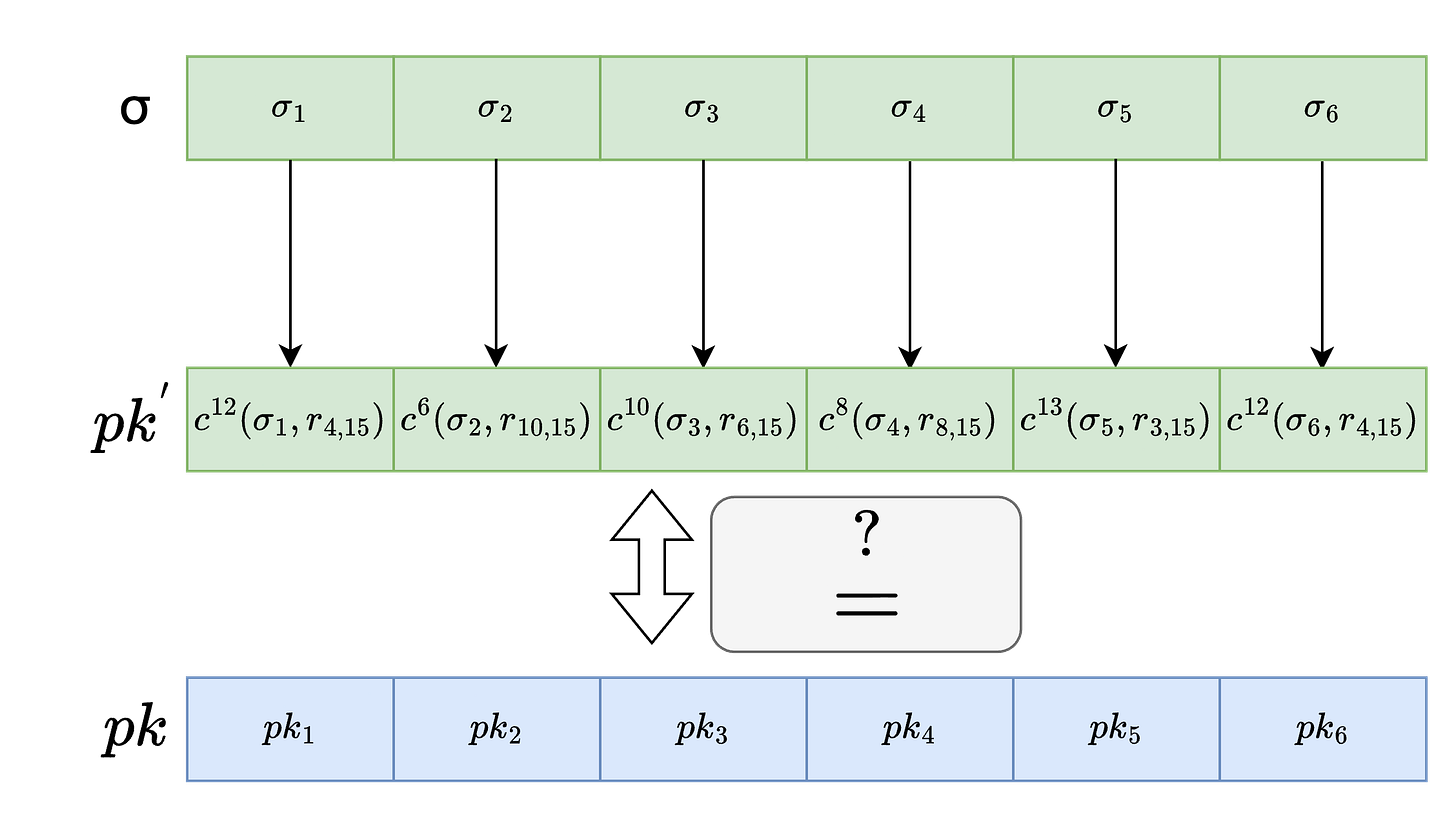
WOTS.Ver(m,pk,σ)

After generating the signature we can now share our message along with our signature and public keys which the verifier will use to verify the signature. Although increasing the amount of hash evaluations affects the signing and verification time negatively however signer has to send much less size of bits to the verifier and signer now has to store much less amount of data-bits securely.

The verifier proceeds with the following computation

\(pk^{'}=pk_1^{'}||pk_2^{'}||......||pk_l^{'}\)

\( =c^{w-1-b_1}(\sigma_1,r_{b_1+1,w-1})|| c^{w-1-b_2}(\sigma_2,r_{b_2+1,w-1})|| ......|| c^{w-1-b_l}(\sigma_1,r_{b_l+1,w-1})\)

\(r_{a,b} \ \text{denotes the substring }(r_a,...,r_b)\text{ of r.}\)

The magic lies in the chaining function’s one-way trick. Although we can calculate cj+1(skᵢ,r) given we have cj(skᵢ,r) by hashing it further however its not possible to calculate cj-1(skᵢ,r). That’s why the signer can confidently share their signature, which is just a list of these chain steps. The verifier takes these signature pieces and hashes them further exactly w−1−bᵢ more times to reach the public key the signer shared. If everything checks out, it matches perfectly! But if someone messes with the signature? The verifier’s math won’t line up with the public key. That’s WOTS keeping things secure, one hash at a time!

Toy-Example

Here’s an example implementation of this scheme where w is taken as 16 and the message is 16-bits long.

\(\text{Using these values of n and w } , l_1 \ and \ l_2 \ \text {come out to be 4 and 2 respectively}\)

\(Therefore\ l=l_1+l_2=6 \)

• Sign

• Ver

Now let's understand the role of checksum here. What if a malicious party tampers with any of the message chunks and then tries to forge the signature for the new message? Say in the above example m₁ is increased from 3 to 5, then the original signature element σ₁ can be changed to c²(σ₁,r) to get a new signature that will verify. However, when m₁ is increased by 2, the checksum is decreased by the same amount. Therefore, if the original checksum was 35, the new checksum would be 33.

Since there is a decrease in the checksum, the corresponding values in its base-w representation will be smaller. This means the attacker would need to compute the chain function in the reverse direction to obtain valid signature elements for the checksum. Since the hash function is one-way, computing the chain function in the opposite direction is computationally infeasible. This is precisely why the checksum provides security against forgery attempts.

• In Winternitz OTS, the signer only has to store l secret keys of n bits each (typically l×256 bits) and send to the verifier l public keys of n bits each, along with a signature comprising l chunks of n bits each (2l×256 bits total).

• In contrast, Lamport OTS requires the signer to store 2n secret keys each n bits in length (2n² = 131,072 bits for n=256) and send to the verifier 2n public keys along with n signature chunks (3n² = 196,608 bits for n=256).l is generally much smaller than m (Depending on the value of w considered) which reduces the bits size stored and shared significantly.

In W-OTS even though increasing the amount of hash evaluations affects the signing and verification time negatively ,however, the signer transmits substantially less data to the verifier and needs to store much less secret key material securely.

Merkle Signature Scheme(MSS)

Both the protocols discussed above have a common drawback, What if we need to sign more than one message? Since both are one time signature schemes, a new set of keys (Lets call them OTS keys )is generated for each message that needs to be signed. Therefore managing keys becomes extremely difficult.

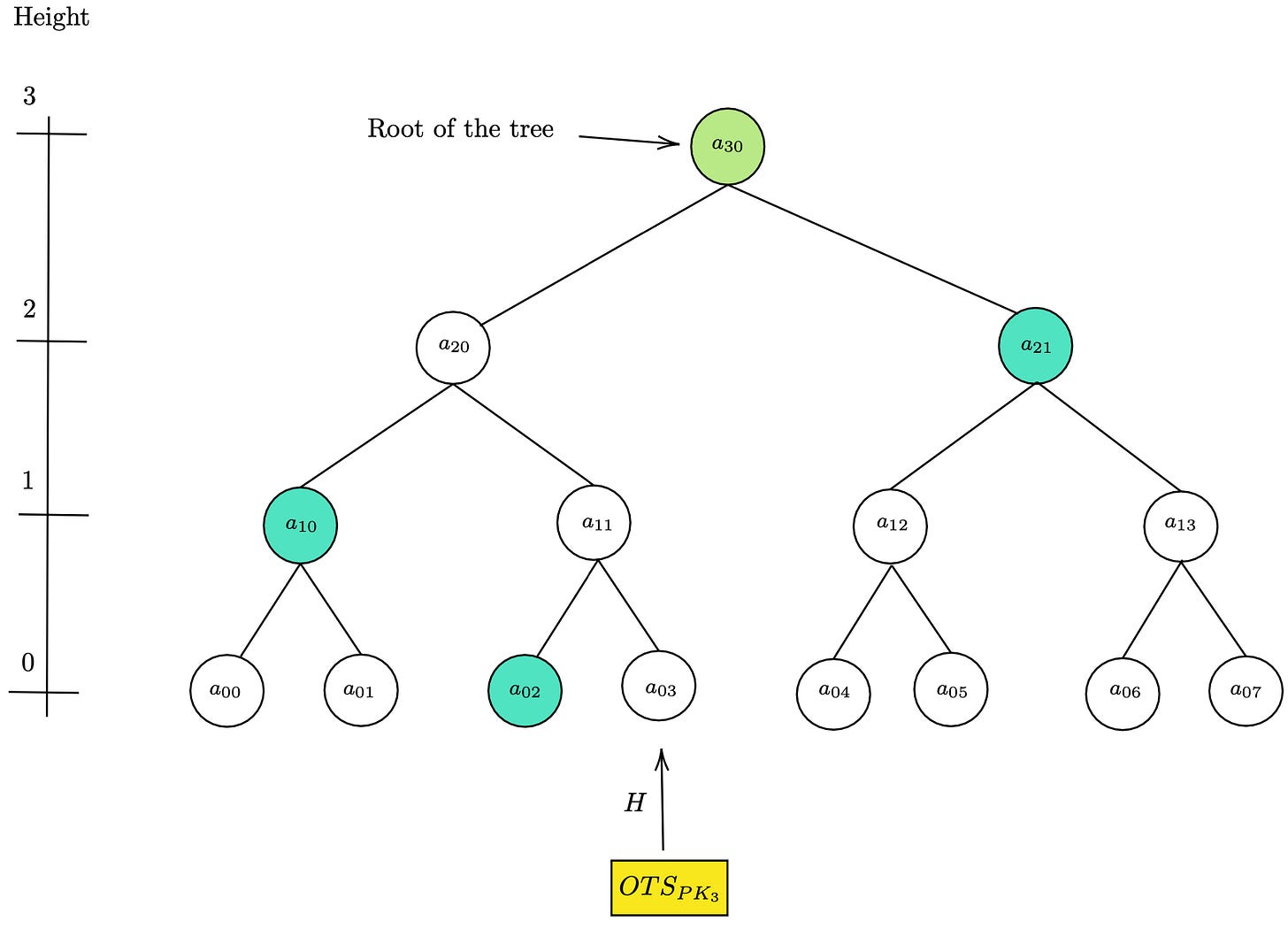
To deal with this issue Ralph Merkle invented MSS. The core idea is to use Merkle Tree leaves to store OTS keys, Merkle trees are binary trees where each parent node is derived by hashing both its child nodes concatenated together. In MSS the leaves are used to store hash of OTS keys.

MSS only gives us a way to efficiently store and manage our keys, it can be used to store keys of both Lamport-OTS and Winternitz-OTS , therefore the below algorithm of MSS is valid for both the schemes and I’ll be giving a generalised approach .

MSS.kg

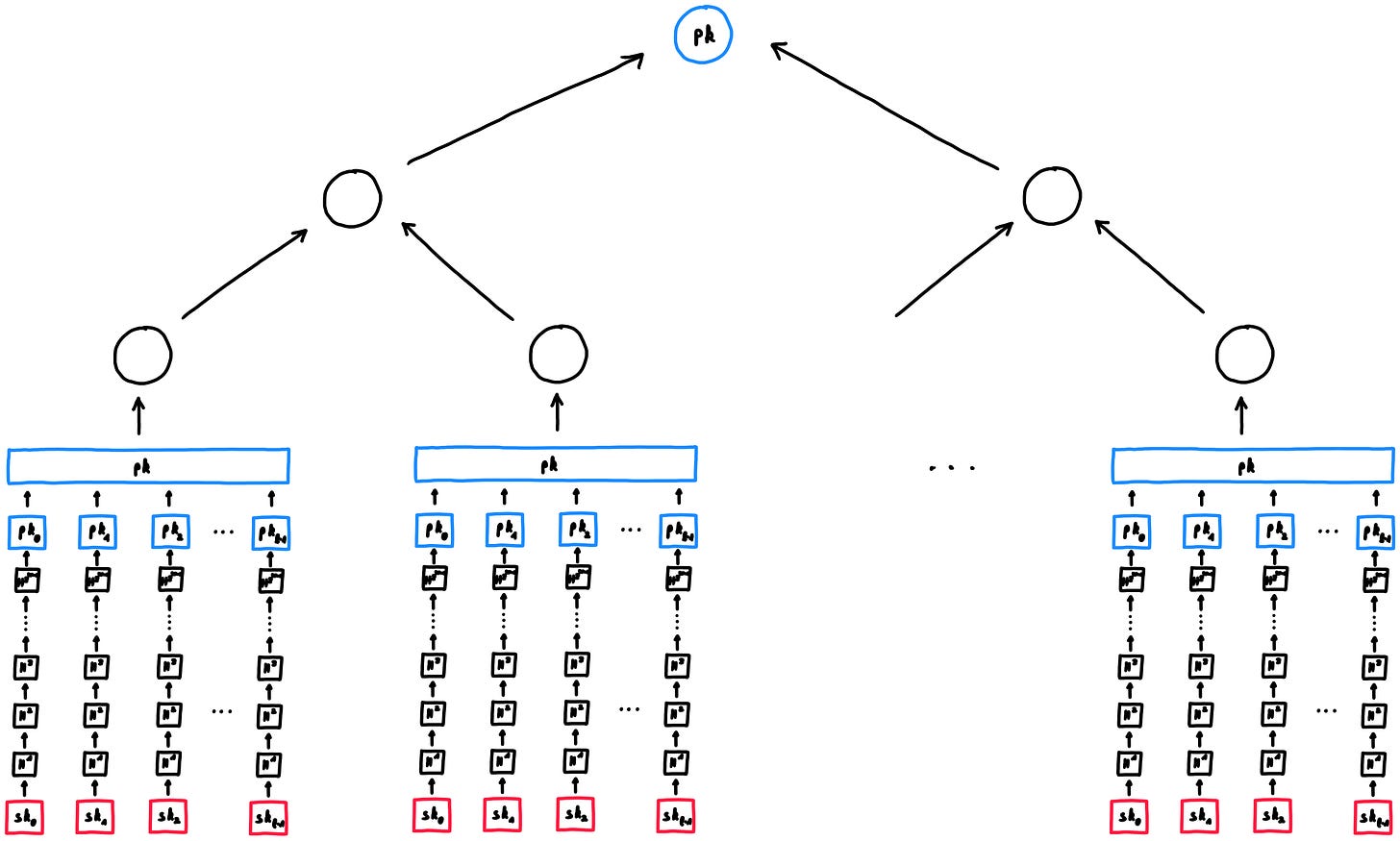
Lets say the keys are being stored in a merkle tree of height n then N=2^n keys can be generated and stored in the merkle tree .Each of the OTS keys can be generated using either of LOTS.kg or WOTS.kg. The hash of the public keys hᵢ is then stored in the leaves of merkle tree.

\(key \ pairs \ :\quad (OTS_{pk_1},OTS_{sk_1}),(OTS_{pk_2},OTS_{sk_2}),......,(OTS_{pk_n},OTS_{sk_n})\)

The key pairs are the private key of MSS.

\(h_i=H(OTS_{pk_i}) \quad 0\leq i \leq 2^n-1 \)

\(\text{Let } a_{i,j} \ \text{denote node with height i and position j } \quad i \in \{0,n\} \quad j \in \{0,2^i-1\}\)

\(\text{Then } a_{0,i}=h_i : \text{leaves of the tree }\)

The inner nodes are computed as follows :

\(a_{i,j}=H({a_{i-1,2j}||a_{{i-1},2j+1}})\)

The public key of MSS , pub is the root of the tree i.e the Merkle root

\(pub=a_{n,0}\)

The signer retains all of the public and secret keys for use in signing i.e the private key of MSS needs to be retained along with the public key.

Heres an example of how key generation process looks like when MSS is used with Winternitz OTS.

https://hackmd.io/@pmuens/r1Ehuixtkg#/44

MSS.Sig

When the signer wants to sign a particular message , say Mᵢ the signer selects an unused key pair ,say the ith pair of MSS private key i.e (OTS_pkᵢ, OTS_skᵢ ) . He then signs the message and generates signature σ_OTSᵢ using either of Lamport or Winternitz OTS.

In addition the final signature consists of index i of the leaf along with OTS_pkᵢ and the Authentication path of that leaf which is a list of sibling nodes needed by the verifier to rebuild the Merkle root i.e public key of MSS.

\(\sigma=(i,OTS_{pk_i},\sigma_{OTS_i},Auth_i)\)

MSS.Ver

Along with the signature, the signer also sends the verifier the public key of MSS and the message itself. The verifier first verifies σₒₜₛᵢ using LOTS.Ver or WOTS.Ver (depending on the protocol used by the signer). Only after this step is successful does the verifier proceed to verify the entire signature.

Next, the verifier hashes OTS_pₖᵢ, which should produce the i-th leaf of the Merkle tree, provided the correct key was shared in the signature.

\(a_{0,i}=H(OTS_{pk_i})\)

Then, using Authᵢ, the verifier reconstructs the Merkle root, which is finally compared with the public key of MSS. If they match, the signature is successfully verified.

Instead of sending a new OTS public key for any of the 2^n messages signer shares pub once and reuse it. This slashes communication overhead .In standalone OTS, signer would have to pre-distribute all public keys or send a new one each time.

So why not just share (OTS_pₖᵢ​,σₒₜₛᵢ​​,m) like in standalone OTS ? Why do we need to share the authentication path ? In MSS the verifier only trusts the public key pub shared by the signer earlier, so someone else could create a fake key pair and sign a message using their own key pair. The authentication path links OTS_pₖᵢ to pub , proving it’s part of the Merkle tree. So wouldn’t this increase the communication overhead? Not really, the authentication path comprises of n nodes i.e n hashes only.

Here’s an example of how MSS works for i=3 .

\(Auth_3=(a_{0,2},a_{1,0},a_{2,1})\)

\(\text{The signature is given by } \sigma= (3,OTS_{pk_3},\sigma_{OTS_3},Auth_3)\)

Conclusion

Both Lamport OTS and Winternitz OTS are one-time schemes, MSS addresses the challenge of generating a new set of keys for each message by allowing many one-time keys to be managed under a single public key through the Merkle tree structure, but key management remains a critical consideration in the design of One Time Signature Schemes.

Stay tuned for the next installment in this blog series, where we will delve into few-time signature schemes—bridging the gap between one-time use and fully reusable digital signatures, and further exploring the evolving landscape of post-quantum cryptography.

PS: I tried implementing the schemes discussed above and can be found over here

1. https://research.kudelskisecurity.com/2021/08/24/quantum-attack-resource-estimate-using-shors-algorithm-to-break-rsa-vs-dh-dsa-vs-ecc/

2. This process is part of Signature generation algorithm